エクセルでレーベンシュタイン距離

CATツールで一致率とかマッチ率とか、普段何気なく呼んでいるこの数字。

どうやって計算されているのか、気になりませんか？

弊社の開発しているCATOVISでは「レーベンシュタイン距離」というものを使っています。

（おそらく他のCATツールでも、ほとんど同じではないかと思いますが……）

# レーベンシュタイン距離ってなに？

レーベンシュタインさんが考案した、2つの文字列の違いを示す指標のことです。

Wikipedia レーベンシュタイン距離

例えば次の2つの文を見てください。

• これが原文1です。
• それは訳文ではない

上の文（S₁）を下の文（S₂）に一致させるには、挿入／削除／置換を何回すればよいでしょうか。

1. 「こ」を「そ」に置換
2. 「原」を「訳」に置換
3. 「が」を「は」に置換
4. 「1」を削除
5. 「す」を「は」に置換
6. 「。」を「な」に置換
7. 「い」を挿入

の合計7回の操作が必要です。この編集コスト 7 がレーベンシュタイン距離となります。

この計算をプログラムするのですが、Wikipediaのアルゴリズムを見てもチンプンカンプンだったので、Excelで見える化してみました。

# Excelにいれてみる

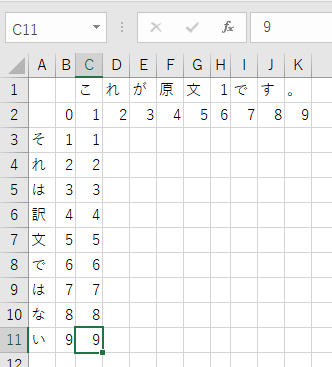
まずはS₁とS₂を1文字ずつセルに入れていきます。まずは列単位でB3から見てみましょう。

S₁の「こ」を「そ」にするには 1回の置換が必要です。

S₁の「こ」を「それ」にするには 1回の置換と1回の挿入が必要です。

S₁の「こ」を「それは」にするには 1回の置換と2回の挿入が必要です

……

と見ていくと、「こ」をS₂に一致させるための操作回数が計算できました。

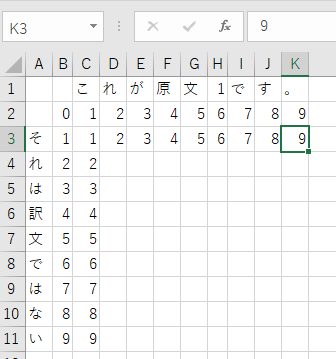
次に行単位です。といっても、さっきと同じこと。

S₂の「そ」を「こ」にするには 1回の置換が必要です。

S₂の「そ」を「これ」にするには 1回の置換と1回の挿入が必要です。

S₂の「そ」を「これが」にするには 1回の置換と2回の挿入が必要です

……

同様に1行目も埋めることができました。

# 計算をはじめる

次に2列目・2行目のD4を見てみます。

ここは「これ」を「それ」に変えるための操作回数を表しています。

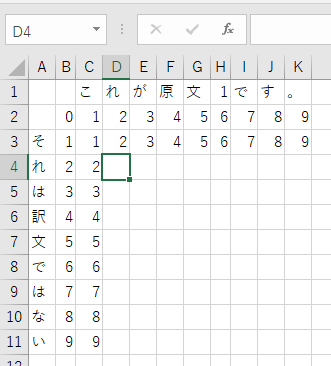
「これ」と「それ」の2文字目は「れ」で一致しているため、新たな操作は発生しません。

そのため、このセルに入れるべき操作回数は、（C3、D3、C4）のうち、最小の数となります。

次に見るのはセルD5。

「これ」を「それは」に変えるには、ここまでの操作回数+1回の挿入が必要になります。

ですので、D5には（C4、D4、C5）のうちの最小数に1を足した数が入ります。

これをExcelの関数で表すと、次のようになります。

=IF(D$1=$A4,MIN(C4,D4,C5),MIN(C4,D4,C5)+1)

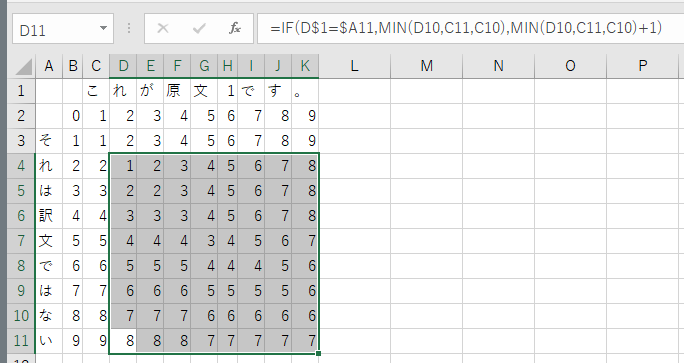
あとはこれを縦横斜めに繰り返すだけ。上記の関数をK11まで貼り付けてしまいましょう。

これで無事に 7 という操作回数にたどり着くことができました。

しかしこのレーベンシュタイン距離（操作回数）は、このままでは使いにくい数字です。

今回のように9文字の文に対して7回操作するのと、100文字の文に7回操作するのは全く意味が異なります。

前者は全く異なる文、後者はかなり似ている文と言えますね。

そのため最後に、S₁とS₂のうち文字数の多い方（今回は同じですが）から操作回数を引き、文字数で割ることで標準化をします。

Excelでは

=(MAX(COUNTA(B1:K1),COUNTA(A2:A11))-K11)/MAX(COUNTA(B1:K1),COUNTA(A2:A11))

ですね。

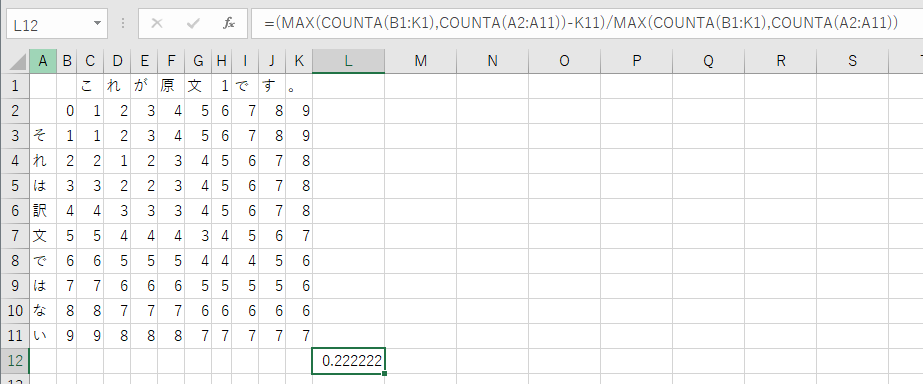
これで無事、一致率の計算過程がExcelで見られるようになりました。

……でも何百、何千と原文やメモリがあるときに、一つずつExcelで表をつくるのは非現実的です。

こんな面倒な計算ですが、Pythonには標準ライブラリに組み込まれています。

さすがですね！

# PR